Hình hộp chữ nhật là một hình học quen thuộc trong cuộc sống. Công thức tính diện tích và Thể tích hình hộp chữ nhật có tính ứng dụng cao. Cùng tìm hiểu chi tiết nội dung này thông qua bài viết dưới đây.
Công thức tính thể tích hình hộp chữ nhật
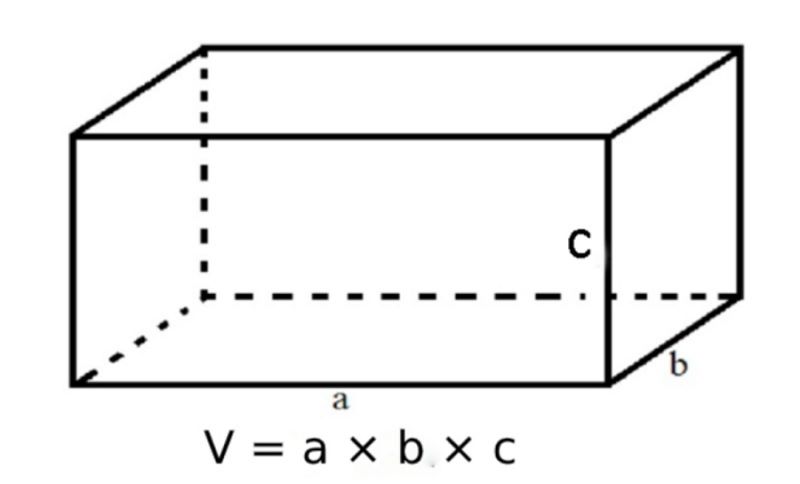
Để tính thể tích của hình hộp chữ nhật, ta lấy tích của chiều dài nhân chiều rộng và chiều cao của hình.
Với hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao lần lượt là a,b, h. Thì công thức tính thể tích hình hộp chữ nhật là:
V = a x b x h
Ví dụ: Tính thể tích hình hộp chữ nhật biết chiều dài 5cm, chiều rộng 4cm và chiều cao là 3cm?
Giải:
Áp dụng công thức tính thể tích hình hộp ta có:
V = 5 x 4 x 3 = 60cm3
Một số dạng bài liên quan đến tính thể tích hình hộp chữ nhật
Dạng 1: Tính thể tích hình hộp khi biết chiều dài, chiều rộng và chiều cao cho trước.
Ví dụ: Một hình chữ nhật có chiều dài 4cm, chiều rộng 3cm và chiều cao 2cm. Tính thể tích của hình hộp chữ nhật đã cho?
V = a x b x h = 4 x 3 x 2 => V = 24cm3
Dạng 2: Tính độ dài một trong ba kích thước của hộp chữ nhật khi bài cho biết thể tích của nó và hai kích thước còn lại.
Ví dụ: Tính chiều rộng của một hình hộp chữ nhật biết thể tích 240cm3, chiều dài 4cm và chiều cao 6cm.
V = a x b x h <=>240 = 4 x b x 6 => b = 10cm

Dạng 3: Tìm chiều cao của hình hộp chữ nhật khi biết thể tích, chiều dài và chiều rộng.
Ví dụ: Tìm chiều cao của hình hộp chữ nhật cho biết thể tích 420cm3, chiều dài 10cm và chiều rộng 6cm.
V = a x b x h <=> 420 = 10 x 6 x h => Chiều cao h = 7cm
Dạng 4: Tính thể tích của một hình hộp chữ nhật khi được cắt bỏ một phần.
Ví dụ: Tính thể tích của hình hộp chữ nhật cho biết chiều dài 12cm, chiều rộng 6cm và chiều cao 3cm nếu như một phần của hộp đã bị cắt bỏ.
V = a x b x h
V = (12 x 6 x 3) – (4 x 3 x 3)
=> V = 648 – 36 = 612cm3
Dạng 5: Tính thể tích của hình hộp chữ nhật có một lỗ hình tròn đã được đục ra khỏi một mặt phẳng của nó.
Ví dụ: Tính thể tích của hình hộp chữ nhật cho biết chiều dài 10cm, chiều rộng 8cm và chiều cao 6cm. Nếu một lỗ hình tròn bán kính 2cm đã được đục ra khỏi một mặt phẳng của nó.
V = a x b x h => V = (10 x 8 x 6) – (pi x 22 x 6)
V = 480 – 75.4 = 404.6cm3
Dạng 6: Tính thể tích của hình hộp chữ nhật không đều, với các mặt phẳng lệch nhau.
Ví dụ: Tính thể tích của một hộp chữ nhật không đều đã cho. Với chiều dài 10cm, chiều rộng 5cm và chiều cao 4cm. Mặt phẳng dưới cùng của hình hộp là một hình tam giác đều có cạnh 6cm.
V = a x b x h => V = (10 x 5 x 4) + (½ x 6 x 4)
V = 200 + 12 = 212cm3
Tham khảo: Bảng chữ cái tiếng Hàn
Những lưu ý khi tính thể tích
Trong quá trình tính toán thể tích hình hộp, có một số điểm lưu ý quan trọng sau:
Đảm bảo rằng tất cả các kích thước trong hình hộp (chiều dài, chiều rộng, và chiều cao) đều được đo bằng cùng một đơn vị. Nếu không, bạn cần thao tác chuyển đổi tất cả các kích thước về cùng một đơn vị trước khi thực hiện tính toán.
Khi tính thể tích, kết quả thu được cũng cần cùng một đơn vị khối tương ứng (ví dụ: m3, cm3).
Trong các trường hợp, sử dụng các số đo có độ chính xác cao hay phức tạp (ví dụ: số thập phân hoặc phân số). Khi này cần chú ý đến việc làm tròn số để đảm bảo rằng kết quả cuối cùng hợp lý và chính xác.
Áp dụng công thức đúng đắn trong một số trường hợp cụ thể. Ví dụ, khi hình hộp chữ nhật với các mặt không phải là hình chữ nhật hoàn hảo (nó có thể do biến dạng). Khi này cần cân nhắc lại việc áp dụng công thức trên một cách đúng đắn.
Việc nắm vững những lưu ý trên đây sẽ giúp bạn tính toán thể tích một cách chính xác. Đồng thời giúp bạn áp dụng linh hoạt công thức trong các tình huống thực tế khác nhau.
Ứng dụng của công thức tính thể tích hình hộp trong thực tế
Việc tính thể tích của hình hộp chữ nhật có nhiều ứng dụng quan trọng trong cuộc sống và công nghệ. Dưới đây là một số ví dụ nổi bật:
Trong xây dựng và kiến trúc: Dùng tính thể tích của phòng, bể bơi, hoặc bất kỳ cấu trúc nào giúp xác định được lượng vật liệu cần thiết hoặc khả năng chứa đựng của không gian.
Trong vận chuyển: Tính thể tích của các container vận chuyển dùng để tối ưu hóa việc sắp xếp và vận chuyển hàng hóa. Từ đó, giảm chi phí và tăng hiệu quả.
Trong khoa học và kỹ thuật: Việc tính thể tích của các bộ phận máy móc, thiết bị. Từ đó, xác định dung tích, sức chứa, hoặc dùng để thiết kế với độ chính xác cao.
Trong giáo dục: Dạy học sinh, sinh viên về các khái niệm không gian và công thức thể tích. Từ đó, họ sẽ hiểu rõ hơn về thế giới xung quanh qua việc áp dụng toán học vào đời sống thực tiễn.
Trong cuộc sống hàng ngày: Tính toán không gian lưu trữ cho kho xưởng, nhà ở hoặc văn phòng. Ví dụ như tủ sách, tủ lạnh, hoặc thùng chứa.
Có thể nói, Công thức để tính thể tích của hình hộp chữ nhật là công cụ không thể thiếu trong nhiều lĩnh vực. Từ đó, giải quyết các vấn đề hàng ngày đến ứng dụng trong những dự án phức tạp hơn.






