Diện tích tam giác cân
Tam giác cân là gì? Tính chất tam giác cân
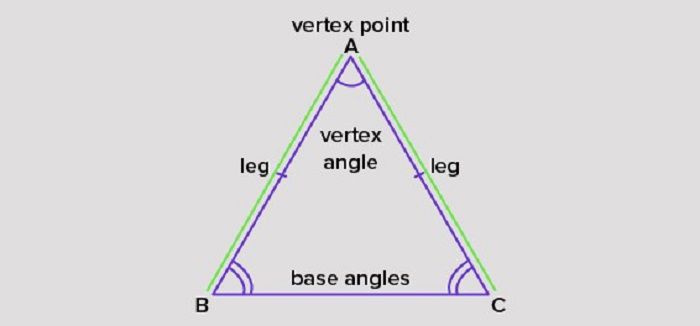
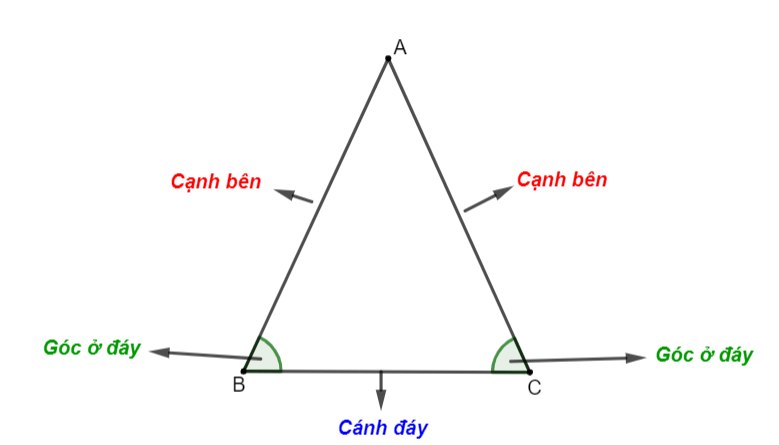
Một tam giác được gọi là tam giác cân khi có hai cạnh có độ dài bằng nhau. Hai cạnh bằng nhau đó gọi là cạnh bên, góc đối diện với cạnh bên gọi là góc ở đỉnh, và cạnh còn lại gọi là đáy.
Các tính chất của tam giác cân
Trong tam giác cân, hai góc nằm ở đáy có số đo bằng nhau.
Đường trung trực của đáy: Đường trung trực của đáy đồng thời là đường cao, đường phân giác và đường trung tuyến ứng với cạnh đáy.
Tam giác cân nội tiếp đường tròn: Mọi tam giác cân đều có thể nội tiếp một đường tròn, với tâm đường tròn là trung điểm của cạnh đáy.
Vì sao tam giác cân có những tính chất này?
Tính chất đối xứng: Tam giác cân có trục đối xứng là đường trung trực của đáy. Chính vì tính đối xứng này mà các góc ở đáy bằng nhau và đường trung trực cũng đồng thời là đường cao, đường phân giác và đường trung tuyến.
Tam giác cân
Công thức tính diện tích tam giác cân
Để tính diện tích tam giác cân, chúng ta sử dụng công thức chung cho mọi tam giác:
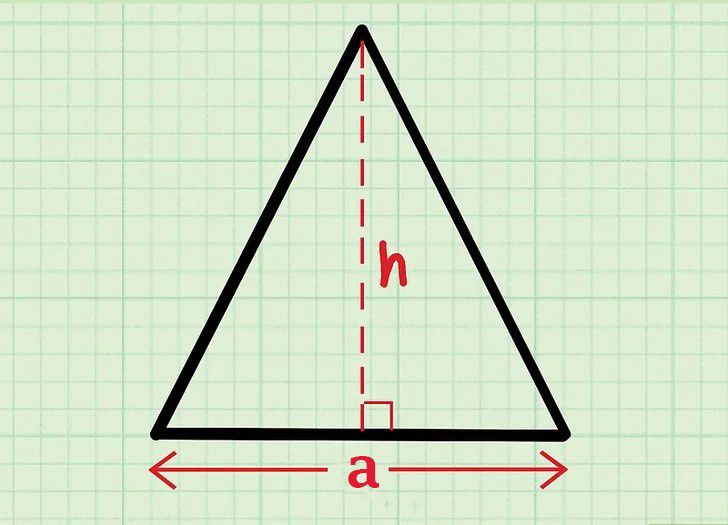
S = (a x h) / 2
Trong đó:
S: Diện tích tam giác cân
a: Độ dài đáy của tam giác (cạnh không bằng hai cạnh bên)
h: Chiều cao tương ứng với đáy (độ dài đoạn thẳng vuông góc kẻ từ đỉnh đối diện xuống đáy)
Tại sao lại như vậy?
Bất kể là tam giác cân hay tam giác thường, diện tích của nó luôn bằng một nửa tích của đáy và chiều cao tương ứng. Vì vậy, công thức trên áp dụng cho mọi loại tam giác, bao gồm cả tam giác cân. Cách tính diện tích của tam giác cân khá đơn giản và có thể áp dụng dễ dàng.
Tam giác cân
Các loại tam giác thường gặp
Các tam giác được chia loại theo độ dài các cạnh và số đo các góc. Sau đây là một số loại tam giác thường gặp:
Tam giác thường
Không có cạnh nào bằng nhau.
Các góc không bằng nhau.
Tam giác cân
Có hai cạnh bằng nhau.
Trong một tam giác, nếu hai cạnh bằng nhau thì hai góc đối diện với chúng cũng bằng nhau.
Tam giác đều
Cả ba cạnh bằng nhau.
Cả ba góc đều bằng 60 độ.
Tam giác vuông
Có một góc vuông (bằng 90 độ).
Trong tam giác vuông, cạnh dài nhất đối diện với góc vuông được gọi là cạnh huyền.
Hai cạnh còn lại gọi là cạnh góc vuông.
Tam giác vuông cân
Là tam giác vừa vuông, vừa cân.
Hai cạnh góc vuông bằng nhau.
Hai góc nhọn đều bằng 45 độ.
Tam giác tù
Có một góc lớn hơn 90 độ.
Tam giác nhọn
Cả ba góc đều nhỏ hơn 90 độ.
Tính chất chung của tam giác
Tổng ba góc trong một tam giác bằng 180 độ.
Tổng độ dài của hai cạnh bất kỳ trong tam giác luôn lớn hơn độ dài cạnh còn lại.
Các đường đặc biệt trong tam giác
Đường trung trực: Đường vuông góc với một cạnh tại trung điểm của cạnh đó.
Đường cao: Đoạn thẳng vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện.
Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện.
Đường phân giác: Tia phân giác của một góc trong tam giác.
Tham khảo: Bảng đơn vị đo độ dài lớp 3
Tam giác cân
Bài tập về tam giác
Bài tập 1: Tam giác thường
Cho tam giác ABC có AB = 5cm, AC = 7cm, BC = 8cm.
- a) Hãy chứng minh rằng tam giác ABC là một tam giác vuông.
- b) Tính diện tích tam giác ABC.
- c) Vẽ đường cao AH. Tính độ dài AH.
Bài tập 2: Tam giác cân
Cho tam giác ABC cân tại A, biết rằng góc B có số đo 50 độ.
- a) Tính số đo góc C.
- b) Kẻ đường cao AH. Chứng minh AH đồng thời là đường trung tuyến, đường phân giác của tam giác ABC.
Bài tập 3: Tam giác đều
Cho tam giác ABC đều cạnh a.
- a) Tính chiều cao của tam giác ABC.
- b) Tính diện tích tam giác ABC.
Bài tập 4: Tính chất đường trung tuyến
Trong tam giác ABC, ba đường trung tuyến AM, BN, CP giao nhau tại điểm G. Chứng minh:
- a) GA = 2/3 AM
- b) BN + CP > 3/2 BC
Bài tập 5: Bài toán thực tế
Một mảnh đất hình tam giác có hai cạnh bằng nhau và một góc bằng 60 độ. Biết cạnh bên dài 10m. Tính diện tích mảnh đất đó.
Bài tập 6: Tam giác vuông cân
Cho tam giác ABC vuông cân tại A, có cạnh huyền BC = 8cm. Hãy xác định độ dài của cạnh AB và tính diện tích của tam giác ABC.
Bài tập 7: Tam giác đều và đường cao
Xét tam giác đều ABC với cạnh có độ dài 6cm. Vẽ đường cao AH. Hãy tính chiều dài của đoạn AH và diện tích của tam giác ABC.
Bài tập 8: Bài toán thực tế
Một mảnh đất hình tam giác có hai cạnh bằng nhau và một góc bằng 60 độ. Biết cạnh bên dài 10m. Tính diện tích mảnh đất đó.
Bài tập 9: Tính chất đường trung tuyến
Trong tam giác ABC, ba đường trung tuyến AM, BN, CP giao nhau tại điểm G. Chứng minh:
- a) GA = 2/3 AM
- b) BN + CP > 3/2 BC
Bài tập 10: Bài toán tổng hợp
Cho tam giác ABC cân tại A. Kẻ đường cao AH.
- a) Chứng minh tam giác ABH = tam giác ACH.
- b) Cho biết AB = 10cm, AH = 8cm. Tính độ dài BC.
- c) Kẻ HM vuông góc với AB (M thuộc AB), HN vuông góc với AC (N thuộc AC). Chứng minh MN // BC.
Gợi ý giải
Vẽ hình: Vẽ hình minh họa sẽ giúp bạn hình dung rõ hơn về bài toán.
Phân tích bài toán: Xác định loại tam giác, các yếu tố đã biết và yêu cầu của bài toán.
Áp dụng định lý, công thức: Sử dụng các định lý, công thức về tam giác để giải bài toán.
Kiểm tra lại kết quả: Sau khi tính toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Một số lưu ý
Đọc kỹ đề bài: Hiểu rõ yêu cầu của bài toán.
Vẽ hình: Vẽ hình tỉ lệ sẽ giúp bạn dễ dàng hình dung và giải bài toán hơn.
Sử dụng các công thức: Áp dụng các công thức tính diện tích, tính góc, tính độ dài đoạn thẳng… một cách chính xác.
Kiểm tra lại đơn vị đo: Đảm bảo các đơn vị đo được sử dụng thống nhất.
Trên đây là một số thông tin về công thức tính diện tích tam giác cân. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.






