Công thức tính đường kính hình tròn có nhiều ứng dụng quan trọng trong toán học, kỹ thuật, xây dựng, thiên văn học, y học, công nghệ và đời sống hàng ngày. Cùng tìm hiểu chi tiết qua bài viết dưới đây nhé!
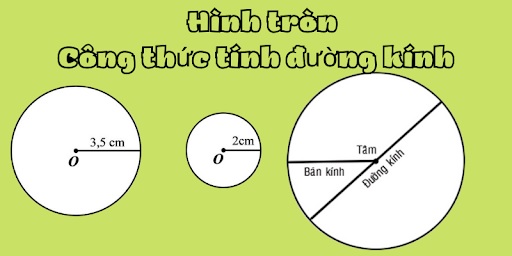
Công thức tính đường kính hình tròn
Định nghĩa đường kính hình tròn
Đường kính của hình tròn là một đoạn thẳng dài nhất nối hai điểm nằm trên đường tròn và đi qua tâm của nó. Đường kính chia hình tròn thành hai phần bằng nhau và luôn vuông góc với mọi bán kính cắt nó tại tâm.
Công thức tính đường kính hình tròn
Đường kính của hình tròn là đoạn thẳng dài nhất nối hai điểm trên đường tròn và đi qua tâm của nó. Đường kính được ký hiệu là ddd và có thể được tính bằng nhiều cách khác nhau tùy vào dữ kiện có sẵn như bán kính, chu vi hoặc diện tích của hình tròn. Dưới đây là các công thức phổ biến để tính đường kính hình tròn:
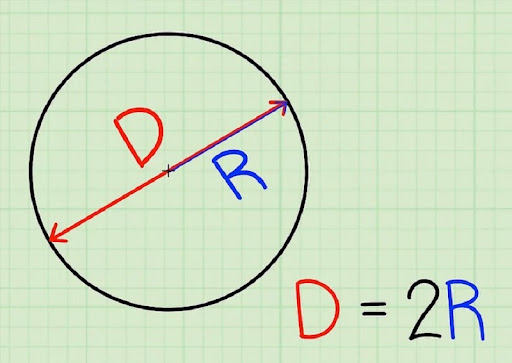
- Công thức tính đường kính dựa vào bán kính
Bán kính của hình tròn là khoảng cách từ tâm đến một điểm bất kỳ trên đường tròn. Đường kính có độ dài gấp đôi bán kính, vì vậy ta có công thức:
Công thức:
🔹 d=2r
Trong đó:
- d là đường kính của hình tròn.
- r là bán kính của hình tròn.
📌 Ví dụ: Nếu bán kính của một hình tròn là 5 cm, thì đường kính sẽ là:
d=2×5=10 cm.
- Công thức tính đường kính dựa vào chu vi
Chu vi của hình tròn là độ dài đường biên của nó, được tính bằng công thức:
C=πd
Từ đó, ta có công thức tính đường kính theo chu vi:
Công thức:
🔹 d=C/π
Trong đó:
- d là đường kính của hình tròn.
- C là chu vi của hình tròn.
- π là hằng số toán học (≈ 3.1416).
📌 Ví dụ: Nếu một hình tròn có chu vi 31.4 cm, thì đường kính sẽ là:
d=31.4/3.1416≈10 cm.
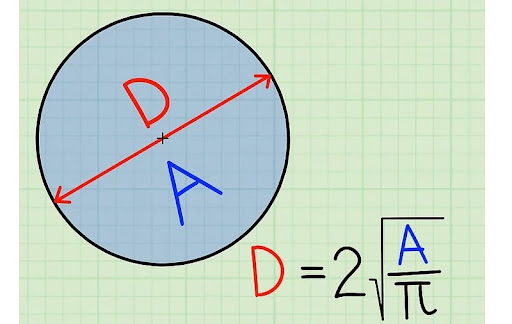
- Công thức tính đường kính dựa vào diện tích
Diện tích của hình tròn được tính theo công thức:
S=πr²
Từ đó, ta có công thức tính đường kính theo diện tích:
Công thức:
🔹 d=2×√S/π
Trong đó:
- d là đường kính của hình tròn.
- S là diện tích của hình tròn.
- π là hằng số toán học (≈ 3.1416).
📌 Ví dụ: Nếu một hình tròn có diện tích 78.5 cm², thì đường kính sẽ là:
d=2×√78.5/3.1416=2×√25=2×5=10 cm
Việc tính toán đường kính của hình tròn có thể được thực hiện dễ dàng bằng cách sử dụng các công thức trên. Tùy vào dữ kiện có sẵn (bán kính, chu vi hoặc diện tích), bạn có thể lựa chọn công thức phù hợp nhất. Các công thức này không chỉ được sử dụng trong toán học mà còn có nhiều ứng dụng thực tế trong kỹ thuật, kiến trúc, cơ khí và nhiều lĩnh vực khác.
Tham khảo: Kích thước ống hdpe
Ứng dụng của công thức tính đường kính
Công thức tính đường kính hình tròn là một trong những công thức quan trọng trong toán học và thực tiễn. Việc hiểu và áp dụng công thức này giúp giải quyết nhiều vấn đề liên quan đến đo lường, thiết kế và tính toán trong nhiều lĩnh vực khác nhau như kỹ thuật, xây dựng, thiên văn học, y học và công nghệ. Dưới đây là một số ứng dụng cụ thể của công thức này.
- Ứng dụng trong toán học và hình học
Trong toán học, công thức tính đường kính giúp xác định mối quan hệ giữa các yếu tố của hình tròn như bán kính, chu vi và diện tích. Đây là nền tảng quan trọng để giải quyết các bài toán hình học liên quan đến đường tròn, hình cầu và các đối tượng có dạng tròn. Bên cạnh đó, công thức này cũng đóng vai trò quan trọng trong các chứng minh hình học, giúp suy ra các định lý liên quan đến đường tròn và ứng dụng trong thực tế.
- Ứng dụng trong kỹ thuật và cơ khí
Trong lĩnh vực kỹ thuật và cơ khí, công thức tính đường kính được sử dụng để thiết kế và chế tạo các bộ phận máy móc có dạng hình tròn, như bánh răng, trục quay, vòng bi, bánh xe và các chi tiết khác. Kích thước của các bộ phận này ảnh hưởng trực tiếp đến hiệu suất và độ bền của máy móc. Ngoài ra, trong công nghiệp sản xuất, việc xác định đường kính của các ống dẫn khí, ống dẫn nước, dây cáp điện và các vật liệu hình tròn khác là rất quan trọng để đảm bảo tính toán chính xác và tối ưu hóa quá trình sản xuất.
- Ứng dụng trong xây dựng và kiến trúc
Trong ngành xây dựng, công thức tính đường kính được sử dụng để thiết kế và thi công các công trình có dạng hình tròn như cầu tròn, mái vòm, sân vận động, bể chứa nước, hố ga, giếng nước, ống thoát nước và nhiều cấu trúc khác. Việc tính toán đường kính giúp đảm bảo độ chính xác trong thiết kế, từ đó tăng cường tính an toàn và ổn định của công trình. Ngoài ra, công thức này cũng được sử dụng trong việc quy hoạch và thi công các công trình đường bộ, đặc biệt là khi thiết kế các vòng xuyến và giao lộ hình tròn.
- Ứng dụng trong thiên văn học
Trong lĩnh vực thiên văn học, công thức tính đường kính được sử dụng để đo lường kích thước của các hành tinh, mặt trăng, mặt trời và các thiên thể khác. Đường kính của các hành tinh và sao giúp các nhà khoa học nghiên cứu về cấu trúc, khối lượng, mật độ và quỹ đạo của chúng. Ngoài ra, đường kính còn được sử dụng để tính toán khoảng cách giữa các thiên thể, từ đó giúp xác định vị trí và chuyển động của chúng trong vũ trụ.
- Ứng dụng trong y học và sinh học
Trong y học và sinh học, công thức tính đường kính được sử dụng để đo kích thước của tế bào, vi khuẩn, virus và các vi sinh vật khác dưới kính hiển vi. Ngoài ra, trong ngành y học, đường kính của mạch máu, khí quản và các ống dẫn trong cơ thể người cũng đóng vai trò quan trọng trong việc chẩn đoán và điều trị bệnh. Các thiết bị y tế như ống tiêm, ống dẫn dịch, dụng cụ phẫu thuật cũng được thiết kế dựa trên kích thước đường kính phù hợp để đảm bảo an toàn và hiệu quả trong quá trình sử dụng.
- Ứng dụng trong công nghệ và thiết kế sản phẩm
Trong ngành công nghệ và thiết kế sản phẩm, công thức tính đường kính được sử dụng để thiết kế và sản xuất các thiết bị điện tử, linh kiện máy móc, đồng hồ, nắp chai, đĩa CD, bánh răng và nhiều sản phẩm khác có dạng hình tròn. Ngoài ra, trong ngành công nghiệp ô tô, máy bay và tàu vũ trụ, việc tính toán đường kính của các bộ phận như bánh xe, động cơ, hệ thống truyền động là rất quan trọng để đảm bảo hiệu suất hoạt động tối ưu.
- Ứng dụng trong đời sống hàng ngày
Trong cuộc sống hàng ngày, công thức tính đường kính giúp con người đo lường và xác định kích thước của nhiều vật dụng quen thuộc như bàn ghế, nắp nồi, bánh xe đạp, vòng cổ, khung tranh và nhiều đồ vật khác. Ngoài ra, công thức này cũng được sử dụng trong các hoạt động như cắt bánh, thiết kế nội thất, đo lường đường kính của các vật dụng gia đình để lựa chọn kích thước phù hợp.
Công thức tính đường kính hình tròn có nhiều ứng dụng quan trọng trong toán học, kỹ thuật, xây dựng, thiên văn học, y học, công nghệ và đời sống hàng ngày. Việc hiểu và áp dụng công thức này giúp con người giải quyết nhiều vấn đề liên quan đến đo lường, thiết kế và tính toán, từ đó góp phần nâng cao hiệu suất và độ chính xác trong nhiều lĩnh vực khác nhau.
Kết luận
Trên đây, TRƯỜNG THỊNH đã giới thiệu chi tiết về công thức tính đường kính hình tròn, bao gồm định nghĩa, công thức tính toán cũng như các ứng dụng thực tiễn trong nhiều lĩnh vực như toán học, kỹ thuật, xây dựng, thiên văn học, y học và đời sống hàng ngày. Công thức này không chỉ giúp chúng ta xác định kích thước của các hình tròn mà còn đóng vai trò quan trọng trong việc thiết kế, đo lường và tối ưu hóa nhiều công trình, sản phẩm.
Hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin hữu ích, giúp bạn hiểu rõ hơn về đường kính hình tròn và cách ứng dụng công thức này một cách hiệu quả trong thực tế. Chúc bạn học tập và áp dụng thành công!






