Định lý pytago là gì?
Định lý Pytago là một trong những định lý cơ bản và quan trọng nhất trong hình học Euclid, liên quan đến các tam giác vuông. Định lý này phát biểu rằng:
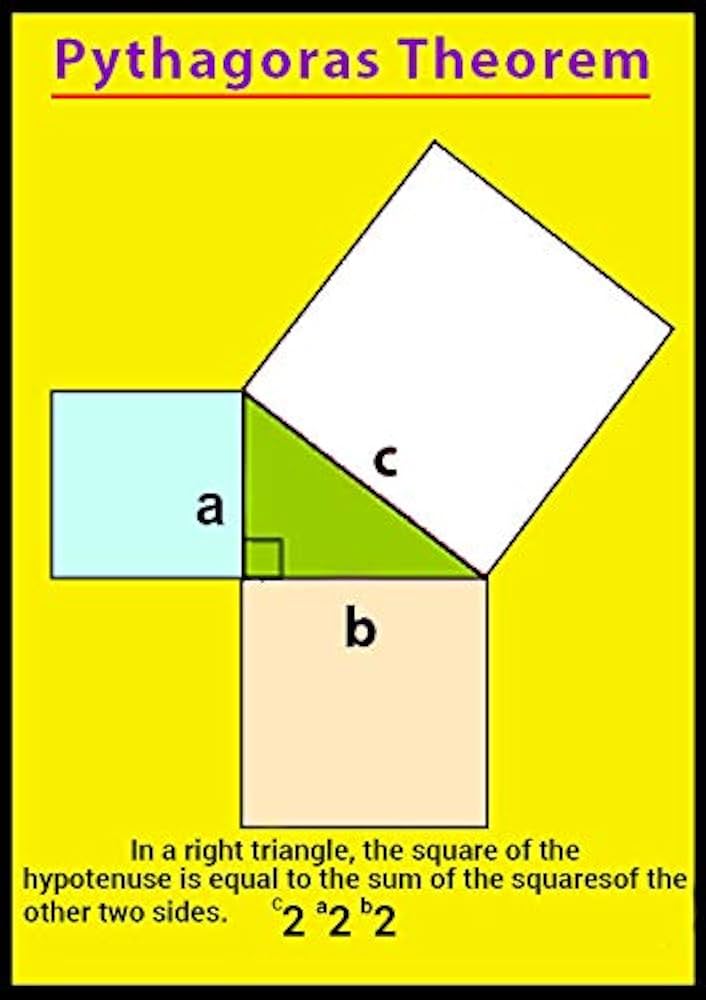
Trong một tam giác vuông, bình phương độ dài cạnh huyền (cạnh dài nhất, đối diện góc vuông) bằng tổng bình phương độ dài hai cạnh còn lại (hai cạnh góc vuông).
Ý nghĩa hình học:
Định lý Pytago mô tả một mối quan hệ cố định giữa ba cạnh của tam giác vuông. Nó không chỉ là một công cụ để tính toán độ dài cạnh còn thiếu trong một tam giác vuông, mà còn là nền tảng cho nhiều khái niệm toán học cao cấp hơn, như khoảng cách trong hệ tọa độ, vectơ, và thậm chí cả định lý trong không gian ba chiều.

Lịch sử ngắn gọn:
Định lý được đặt theo tên nhà toán học người Hy Lạp Pythagoras (khoảng thế kỷ VI TCN), dù thực tế, các nhà toán học ở Babylon và Ấn Độ cổ đại cũng đã biết đến mối quan hệ này trước đó. Tuy nhiên, Pythagoras được cho là người đầu tiên chứng minh nó một cách có hệ thống.
Công thức tổng quát của định lý là:
a² + b² = c²
Trong đó:
- c là cạnh huyền (cạnh đối diện góc vuông),
- a và b là hai cạnh góc vuông của tam giác.

Tại sao định lý pytago lại quan trọng
Định lý Pytago quan trọng không chỉ vì nó là một kết quả đẹp trong toán học, mà còn vì tính ứng dụng rộng lớn và vai trò nền tảng của nó trong rất nhiều lĩnh vực.
Nền tảng của hình học Euclid
Pythagoras là một trong những định lý cơ bản nhất của hình học phẳng. Nó được dùng để tính độ dài cạnh còn lại trong tam giác vuông khi biết hai cạnh còn lại. Từ đó, ta có thể giải các bài toán về độ dài, diện tích, góc nghiêng, đường chéo, v.v.
Gắn liền với tư duy không gian
Định lý giúp ta hiểu rõ hơn về mối quan hệ giữa các cạnh trong không gian hai chiều và ba chiều. Nó là cơ sở để tính khoảng cách giữa hai điểm, kể cả trong hệ trục tọa độ hoặc trong không gian ba chiều.
Ứng dụng trong đời sống và kỹ thuật
- Trong xây dựng: dùng để kiểm tra độ vuông góc, dựng khung nhà, đo đạc thực địa.
- Trong trắc địa và địa lý: tính khoảng cách giữa hai điểm mà không thể đo trực tiếp.
- Trong đồ họa máy tính và lập trình: dùng để tính khoảng cách, dựng hình, mô phỏng vật thể di chuyển.
- Trong vật lý và cơ học: phân tích chuyển động, lực theo các trục.
Là bước đệm cho các kiến thức nâng cao
Từ Pythagoras, ta mở rộng ra nhiều kiến thức như:
- Định lý cos, định lý sin trong tam giác bất kỳ,
- Tính độ dài véc-tơ, tích vô hướng,
- Khoảng cách trong không gian ba chiều,
- Các ứng dụng trong đại số tuyến tính và hình học giải tích.
Tính phổ quát và dễ tiếp cận
Đây là một định lý dễ hiểu, dễ nhớ và có thể minh họa trực quan. Nó được dạy ở cấp THCS nhưng vẫn được dùng trong các ngành kỹ thuật, khoa học máy tính, kiến trúc, vật lý, và nhiều lĩnh vực khác.
Tham khảo: 1 khối nước là bao nhiêu lít?
Ứng dụng của định lý Pythagoras
Định lý Pythagoras, phát biểu rằng trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông, là một trong những định lý nền tảng và nổi tiếng nhất trong toán học. Không chỉ có ý nghĩa lý thuyết, định lý này còn có rất nhiều ứng dụng quan trọng trong thực tế, trải rộng từ toán học, kỹ thuật đến cuộc sống hàng ngày.
Ứng dụng trong học tập và toán học
Định lý Pythagoras là một phần quan trọng trong chương trình học phổ thông. Nó được sử dụng thường xuyên để:
- Tính độ dài cạnh còn lại trong tam giác vuông khi biết hai cạnh còn lại.
- Giải các bài toán liên quan đến khoảng cách, đặc biệt trong hệ trục tọa độ. Chẳng hạn, khoảng cách giữa hai điểm A(x₁, y₁) và B(x₂, y₂) trong mặt phẳng được tính bằng công thức:
AB = √[(x2 – x1)² + (y2 – y1)²] Đây chính là hệ quả trực tiếp của định lý Pythagoras áp dụng trong mặt phẳng tọa độ.
Ngoài ra, định lý còn là cơ sở cho các công thức nâng cao trong hình học, hình học giải tích, hình học không gian và lượng giác như:
- Định lý Cosin và Sin,
- Công thức vectơ và tích vô hướng,
- Khoảng cách giữa điểm và đường thẳng, điểm và mặt phẳng trong không gian 3 chiều.
Ứng dụng trong xây dựng và kiến trúc
Trong ngành xây dựng, định lý Pythagoras được sử dụng để:
- Kiểm tra độ vuông góc giữa các thành phần của một công trình (tường, sàn, dầm, cột).
- Tạo ra các khung vuông chính xác khi thi công, đặc biệt là khi không có công cụ đo góc chuyên dụng.
Một ứng dụng phổ biến là sử dụng tam giác 3-4-5, bởi vì 3² + 4² = 5² . Thợ xây dựng có thể dùng dây thừng chia thành ba đoạn 3m, 4m và 5m để tạo một góc vuông hoàn hảo trên thực địa.
Ứng dụng trong trắc địa và bản đồ
Trong ngành đo đạc đất đai, định lý Pythagoras giúp tính toán khoảng cách giữa hai điểm mà không thể đo trực tiếp. Khi ta biết độ dài theo phương ngang và phương thẳng đứng (hoặc phương Đông – Tây và Bắc – Nam), định lý này cho phép tính nhanh độ dài đường chéo nối hai điểm.
Trong bản đồ học và định vị GPS, việc xác định vị trí chính xác hoặc đo khoảng cách giữa hai vị trí cũng sử dụng định lý này như một phần trong hệ thống tính toán.
Ứng dụng trong vật lý và kỹ thuật
Trong vật lý, định lý Pythagoras thường được dùng để:
- Tính hợp lực của hai lực vuông góc, hay
- Phân tích chuyển động của vật thể theo phương ngang và phương thẳng đứng.
Ví dụ, nếu một vật thể di chuyển 3m theo phương ngang và 4m theo phương dọc, thì quãng đường thực tế mà vật đi được là:
√3² + √4² = 5m
Trong kỹ thuật cơ khí, công nghiệp, robot và cơ điện tử, định lý Pythagoras giúp thiết kế hệ thống chính xác và điều hướng robot trong không gian.
Ứng dụng trong công nghệ và lập trình
Trong thiết kế đồ họa, game 2D và 3D, định lý Pythagoras giúp tính:
- Khoảng cách giữa hai điểm ảnh,
- Di chuyển vật thể theo đường chéo,
- Quy định va chạm giữa các đối tượng.
Trong lập trình, định lý này cũng xuất hiện trong các thuật toán tìm đường ngắn nhất (như thuật toán A*), tính toán độ tương đồng giữa điểm dữ liệu trong học máy hoặc xử lý ảnh kỹ thuật số.
Ứng dụng trong đời sống hằng ngày
Không cần là kỹ sư hay nhà toán học, người bình thường cũng ứng dụng định lý này trong:
- Đo khoảng cách gián tiếp, ví dụ: chiều cao tòa nhà qua bóng đổ và đoạn thẳng,
- Đóng tủ, làm bàn, xây bếp, kiểm tra xem các góc có vuông không,
- Tính chiều dài dây cột, đường chéo sân, hoặc kích thước cần thiết khi di chuyển vật thể qua không gian chật hẹp.
Kết luận
Từ lớp học đến thực tế đời sống, từ xây dựng đến công nghệ cao, định lý Pythagoras luôn hiện diện như một công cụ mạnh mẽ, đơn giản nhưng cực kỳ hữu ích. Sự đa dạng trong ứng dụng của nó cho thấy rằng đây không chỉ là một định lý toán học đơn thuần mà còn là một cây cầu nối giữa lý thuyết và thực hành, giữa tư duy trừu tượng và nhu cầu thực tiễn.
Qua những chia sẻ trên, Trường Thịnh hy vọng bạn đã có cái nhìn rõ ràng và đầy đủ hơn về Định lý Pythagoras – một định lý nền tảng và giàu ứng dụng trong toán học cũng như cuộc sống. Từ định nghĩa, nguồn gốc, cách chứng minh đến các ứng dụng thực tiễn, tất cả đều góp phần thể hiện vai trò quan trọng của định lý này. Chúc bạn học tốt và luôn giữ vững tinh thần khám phá tri thức cùng Trường Thịnh!






