Thể tích hình hộp chữ nhật
Dấu hiệu nhận biết hình hộp chữ nhật
Hình hộp chữ nhật là một hình khối quen thuộc trong cuộc sống hàng ngày. Nó có mặt ở khắp mọi nơi, từ những chiếc hộp đựng đồ đến các tòa nhà cao tầng. Để dễ dàng nhận biết hình hộp chữ nhật, chúng ta cần nắm rõ các đặc điểm của nó.
Các đặc điểm chính của hình hộp chữ nhật
6 mặt: Hình hộp chữ nhật có 6 mặt, tất cả đều là hình chữ nhật.
12 cạnh: Các cạnh của hình hộp chữ nhật vuông góc với nhau tại các đỉnh.
8 đỉnh: Các đỉnh của hình hộp chữ nhật là giao điểm của các cạnh.
Các mặt đối diện bằng nhau: Các mặt đối diện của hình hộp chữ nhật có cùng hình dạng và kích thước.
Các cạnh đối diện song song và bằng nhau: Các cạnh đối diện của hình hộp chữ nhật song song và có độ dài bằng nhau.
Cách nhận biết hình hộp chữ nhật
Để xác định một vật thể có phải là hình hộp chữ nhật hay không, bạn hãy quan sát các đặc điểm sau:
Kiểm tra số mặt: Đếm số mặt của vật thể. Nếu có 6 mặt thì đó có thể là hình hộp chữ nhật.
Kiểm tra hình dạng các mặt: Kiểm tra xem tất cả các mặt của vật thể có phải là hình chữ nhật hay không.
Kiểm tra các cạnh: Kiểm tra xem các cạnh của vật thể có vuông góc với nhau hay không.
So sánh các mặt đối diện: Kiểm tra xem các mặt đối diện có bằng nhau không.
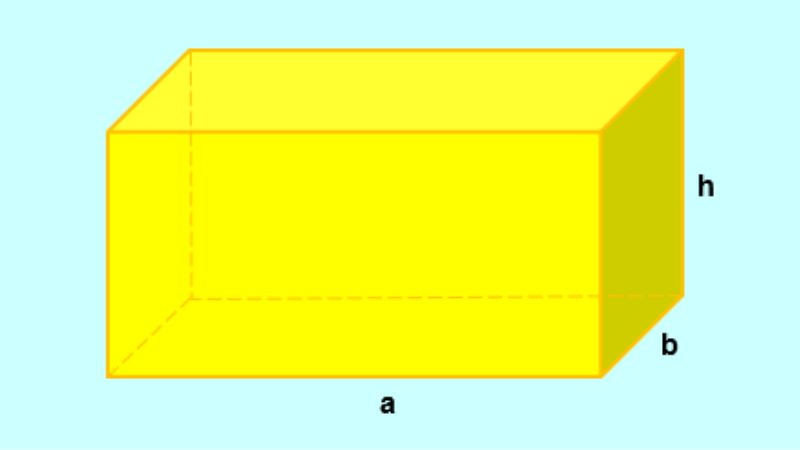
Hình hộp chữ nhật
Công thức tính thể tích hình hộp chữ nhật
Công thức thể tích hình hộp chữ nhật
V = a × b × c
Trong đó:
V: Thể tích của hình hộp chữ nhật (đơn vị đo là mét khối, cm khối,…)
a: Chiều dài của hình hộp chữ nhật
b: Chiều rộng của hình hộp chữ nhật
c: Chiều cao của hình hộp chữ nhật
Ví dụ:
Giả sử chúng ta có một hộp quà hình hộp chữ nhật có chiều dài 30cm, chiều rộng 20cm và chiều cao 15cm. Để tính thể tích của hộp quà, ta áp dụng công thức:
V = 30cm × 20cm × 15cm = 9000 cm³
Vậy thể tích của hộp quà là 9000 cm³.
Tham khảo: Bảng chữ cái tiếng Hàn
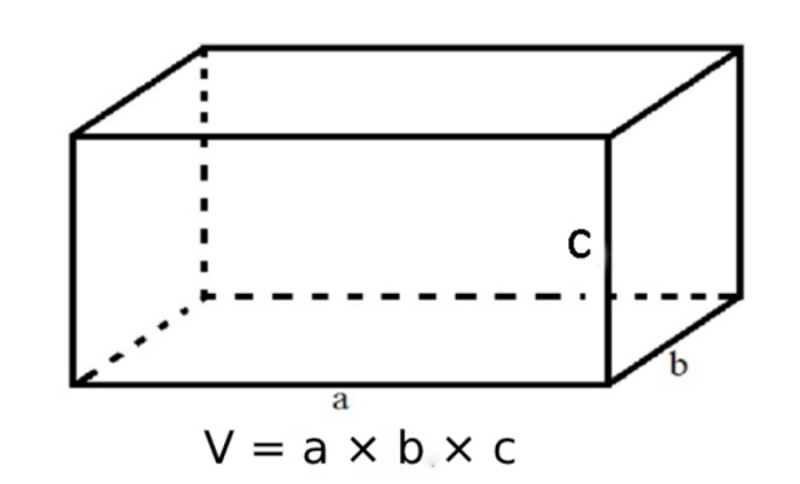
Công thức tính thể tích
Các dạng bài tập về thể tích của hình hộp chữ nhật
Tính thể tích khi biết ba kích thước
Bài toán: Một bể cá hình hộp chữ nhật có chiều dài 80cm, chiều rộng 50cm và chiều cao 40cm. Tính thể tích bể cá.
Cách giải:
Áp dụng công thức: V = a × b × c
V = 80cm × 50cm × 40cm = 160000 cm³ = 160 lít (vì 1dm³ = 1 lít)
Tìm một kích thước khi biết thể tích và các kích thước còn lại
Bài toán: Một bể cá hình hộp chữ nhật có thể tích 120 lít, chiều dài 60cm và chiều rộng 40cm. Tính chiều cao của bể cá.
Cách giải:
Đổi 120 lít = 120 dm³
Áp dụng công thức: c = V / (a × b) = 120 / (60 × 40) = 0.5 dm = 5 cm
Tính thể tích của hình hộp chữ nhật khi biết diện tích đáy và chiều cao
Bài toán: Một hình hộp chữ nhật có diện tích đáy là 20 cm² và chiều cao là 5cm. Tính thể tích hình hộp chữ nhật.
Cách giải:
V = diện tích đáy × chiều cao = 20 cm² × 5cm = 100 cm³
Bài toán liên quan đến đơn vị đo
Bài toán: Một thùng đựng hàng hình hộp chữ nhật có chiều dài 2m, chiều rộng 1,5m và chiều cao 1m. Người ta xếp đầy thùng bằng các hộp hình lập phương cạnh 20cm. Hỏi có bao nhiêu hộp như vậy?
Cách giải:
Tính thể tích thùng hàng và thể tích một hộp.
Chia thể tích thùng hàng cho thể tích một hộp để tìm số hộp.
Bài toán liên quan đến hình học không gian
Bài toán: Cho hình hộp chữ nhật ABCD.A’B’C’D’. Biết AB = 3cm, AD = 4cm, AA’ = 5cm. Tính thể tích hình hộp chữ nhật.
Cách giải:
Áp dụng công thức trực tiếp: V = AB × AD × AA’ = 3cm × 4cm × 5cm = 60 cm³

Bài tập về thể tích
Các bài tập mẫu về thể tích hình hộp
Bài toán 1: Khối gỗ và hình lập phương (tiếp theo)
Đề bài: Một khối gỗ hình hộp chữ nhật có kích thước 12cm x 8cm x 6cm. Người ta muốn sơn toàn bộ bề mặt của khối gỗ đó. Biết rằng cứ 100cm² sơn hết 5000 đồng. Hỏi cần bao nhiêu tiền để sơn hết khối gỗ?
Bài toán 2: Bể cá và đường ống (tiếp theo)
Đề bài: Một bể cá hình hộp chữ nhật có chiều dài 1,2m, chiều rộng 0,8m và chiều cao 0,6m. Người ta mở vòi nước chảy vào bể, mỗi phút chảy được 10 lít nước. Nếu muốn bể đầy nước trong 1 giờ thì mỗi phút vòi nước phải chảy bao nhiêu lít?
Bài toán 3: Hình hộp chữ nhật và hình trụ
Đề bài: Một bể cá hình hộp chữ nhật có kích thước đáy là 60cm x 40cm, chiều cao của bể là 50cm. Người ta thả vào bể một hòn đá, mực nước trong bể dâng lên 2cm. Tính thể tích của hòn đá.
Bài toán 4: Hình hộp chữ nhật và tỉ lệ thuận
Đề bài: Một hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao tỉ lệ với 3, 2, 1. Biết thể tích của hình hộp chữ nhật là 72cm³. Tính kích thước của hình hộp chữ nhật.
Bài toán 5: Ứng dụng thực tế
Đề bài: Một căn phòng hình hộp chữ nhật có chiều dài 6m, chiều rộng 4m và chiều cao 3m. Người ta muốn quét vôi trần nhà và bốn bức tường bên trong phòng. Biết diện tích các cửa là 8m². Tính diện tích cần quét vôi.
Cách học hình học không gian hiệu quả
Nắm vững lý thuyết
Hiểu rõ khái niệm: Hình hộp chữ nhật là gì? Các yếu tố của hình hộp chữ nhật (cạnh, mặt, đỉnh) là gì?
Các công thức: Học thuộc các công thức tính diện tích, thể tích, đường chéo của hình hộp chữ nhật.
Các tính chất: Hiểu rõ các tính chất của hình hộp chữ nhật như các cạnh đối diện song song và bằng nhau, các mặt đối diện song song và bằng nhau.
Vẽ hình
Vẽ hình minh họa: Khi giải bài tập, hãy vẽ hình để trực quan hóa bài toán.
Chú ý tỉ lệ: Hình vẽ không cần quá tỉ mỉ nhưng phải đảm bảo các tỉ lệ chính xác để tránh nhầm lẫn.
Đánh dấu các yếu tố: Đánh dấu các cạnh, góc, đường cao,… lên hình vẽ để dễ dàng theo dõi quá trình giải bài.
Trên đây là một số thông tin về thể tích hình hộp chữ nhật. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.






