Công thức tính đường kính hình tròn
Đường kính, bán kính là gì
Trong hình học, đường tròn là một hình phẳng đặc biệt với các điểm cách đều một điểm trung tâm. Để mô tả kích thước của đường tròn, ta sử dụng hai khái niệm quan trọng: đường kính và bán kính.
Bán kính
Bán kính là đoạn thẳng nối từ tâm của đường tròn đến bất kỳ điểm nào trên đường tròn.
Bán kính thường được ký hiệu là “r”.
Đường kính
Đường kính là đoạn thẳng đi qua tâm của đường tròn và nối hai điểm đối diện trên đường tròn.
Đường kính luôn dài gấp đôi bán kính, và thường được ký hiệu là “d”.
Đường kính là trường hợp đặc biệt của dây cung đi qua tâm.

Hình tròn
Các công thức tính đường kính hình tròn
Đường kính hình tròn là đoạn thẳng đi qua tâm của hình tròn và có hai đầu mút nằm trên đường tròn đó. Đây là một trong những yếu tố cơ bản để xác định kích thước của hình tròn. Công thức tính đường kính hình tròn rất đơn giản và dễ áp dụng:
Công thức tính đường kính hình tròn từ bán kính
d = 2r
Trong đó:
d là đường kính của hình tròn
r là bán kính của hình tròn
Công thức này cho thấy đường kính của hình tròn luôn gấp đôi bán kính của nó. Ngoài ra, nếu bạn biết chu vi của hình tròn, bạn cũng có thể tính đường kính bằng công thức:
Công thức tính đường kính hình tròn từ chu vi
d = C/π
Trong đó:
d là đường kính của hình tròn
C là chu vi của hình tròn
π (pi) là một hằng số có giá trị xấp xỉ 3,14159.
Công thức tính đường kính hình tròn từ diện tích
d = 2 x (√S : √ π)
Trong đó:
d là đường kính của hình tròn
S là diện tích của hình tròn
Tham khảo: Kích thước ống hdpe
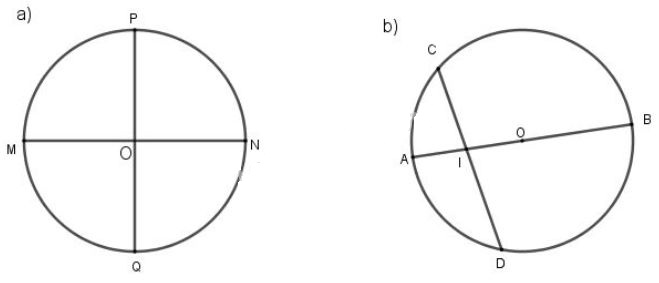
Đường kính, bán hính
Công thức tính chu vi, diện tích hình tròn
Chu vi hình tròn (C)
Chu vi hình tròn là độ dài của đường cong bao quanh hình tròn.
Công thức tính chu vi hình tròn:
C = 2πr (trong đó r là bán kính của hình tròn)
C = πd (trong đó d là đường kính của hình tròn, d = 2r)
Trong đó:
π (pi) là một hằng số toán học, có giá trị xấp xỉ 3.14159.
Diện tích hình tròn (S)
Diện tích hình tròn là phần không gian được giới hạn bởi đường cong của hình tròn.
Công thức tính diện tích hình tròn:
S = πr² (trong đó r là bán kính của hình tròn)
Trong đó:
π (pi) là một hằng số toán học, có giá trị xấp xỉ 3.14159.
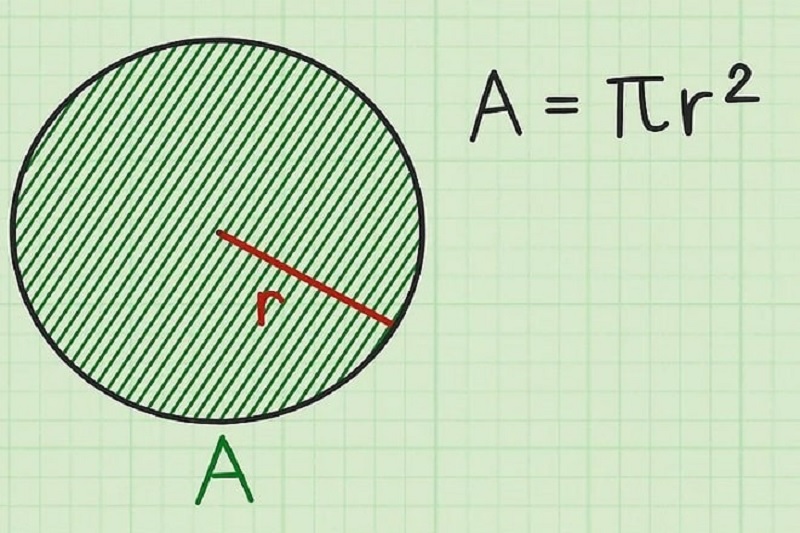
Chu vi diện tích
Các dạng bài tập thường gặp và mẹo làm bài đơn giản
Các dạng bài tập thường gặp
Dạng 1: Tính đường kính khi biết bán kính hoặc ngược lại:
Đây là dạng bài tập cơ bản, áp dụng trực tiếp công thức d = 2r.
Ví dụ: Cho hình tròn có bán kính r = 5 cm, tính đường kính d.
Lời giải: d = 2 * 5 = 10 cm.
Dạng 2: Tính chu vi hình tròn khi biết đường kính hoặc bán kính:
Áp dụng công thức C = πd hoặc C = 2πr.
Ví dụ: Cho hình tròn có đường kính d = 8 cm, tính chu vi C.
Lời giải: C = π * 8 ≈ 25.12 cm.
Dạng 3: Tính diện tích hình tròn khi biết đường kính hoặc bán kính:
Áp dụng công thức A = πr² hoặc A = π(d/2)².
Ví dụ: Cho hình tròn có bán kính r = 6 cm, tính diện tích A.
Lời giải: A = π * 6² ≈ 113.04 cm².
Dạng 4: Bài tập kết hợp với các hình khác:
Các bài tập này thường yêu cầu tính toán liên quan đến hình tròn kết hợp với hình vuông, hình chữ nhật, tam giác,…
Ví dụ: Một hình vuông có cạnh bằng đường kính của hình tròn. Tính diện tích phần nằm ngoài hình tròn nhưng nằm trong hình vuông.
Dạng 5: Bài tập thực tế:
Các bài tập này liên quan đến các tình huống thực tế, chẳng hạn như tính toán diện tích sân tròn, chu vi đường đua,…
Ví dụ: Một sân tròn có đường kính 20 m, tính diện tích sân.
Mẹo làm bài hữu ích
Nắm vững công thức cơ bản:
Đường kính (d) = 2 x Bán kính (r)
Chu vi (C) = πd hoặc C = 2πr
Diện tích (A) = πr²
Biết cách suy luận:
Nếu bài toán cho chu vi, bạn có thể dễ dàng tìm ra đường kính bằng công thức d = C/π.
Nếu bài toán cho diện tích, bạn có thể tìm ra bán kính bằng công thức r = √(A/π), sau đó suy ra đường kính.
Vẽ hình minh họa:
Việc vẽ hình tròn và đánh dấu các yếu tố đã biết sẽ giúp bạn hình dung bài toán rõ ràng hơn, từ đó tìm ra cách giải phù hợp.
Lưu ý đến đơn vị đo:
Đảm bảo rằng tất cả các đơn vị đo đều thống nhất trước khi thực hiện tính toán.
Sử dụng máy tính bỏ túi:
Trong các bài toán phức tạp, sử dụng máy tính bỏ túi sẽ giúp bạn tiết kiệm thời gian và giảm thiểu sai sót.
Bài tập mẫu
Bài tập 1:
Cho hình vuông ABCD có cạnh là 10 cm. Vẽ một hình tròn nội tiếp hình vuông đó. Tính diện tích của phần hình vuông nằm ngoài hình tròn.
Lời giải:
Đường kính của hình tròn nội tiếp bằng cạnh hình vuông, tức là 10 cm.
Bán kính hình tròn là 5 cm.
Diện tích hình tròn là π × (5 cm)² = 25π cm².
Diện tích hình vuông là 10 cm × 10 cm = 100 cm².
Diện tích phần hình vuông nằm ngoài hình tròn là 100 cm² – 25π cm².
Bài tập 2:
Một hình tròn có diện tích là 100π cm². Một hình chữ nhật có chiều dài bằng đường kính hình tròn và chiều rộng bằng bán kính hình tròn. Tính diện tích của hình chữ nhật đó.
Lời giải:
Diện tích hình tròn là π × (Bán kính)² = 100π cm², suy ra Bán kính = 10 cm.
Đường kính hình tròn là 20 cm.
Diện tích hình chữ nhật là 20 cm × 10 cm = 200 cm².
Bài tập 3:
Cho hai hình tròn đồng tâm, hình tròn lớn có bán kính là 8 cm, hình tròn nhỏ có bán kính là 5 cm. Tính diện tích của phần hình tròn lớn nằm ngoài hình tròn nhỏ.
Lời giải:
Diện tích hình tròn lớn là π × (8 cm)² = 64π cm².
Diện tích hình tròn nhỏ là π × (5 cm)² = 25π cm².
Diện tích phần hình tròn lớn nằm ngoài hình tròn nhỏ là 64π cm² – 25π cm² = 39π cm².
Trên đây là một số thông tin về công thức tính đường kính hình tròn. Hi vọng cá bạn sẽ có cho mình thông tin hữu ích.






