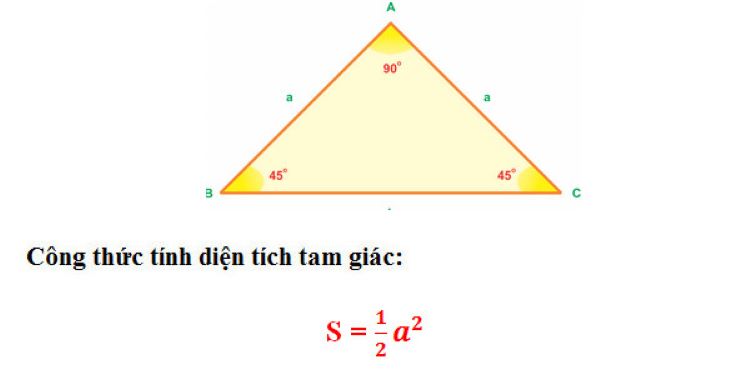
Diện tích tam giác cân
Tính chất cơ bản của tam giác
Các tính chất cơ bản của tam giác
Tổng ba góc trong một tam giác bằng 180 độ: Đây là một tính chất nền tảng và được sử dụng rất nhiều trong các bài toán về tam giác.
Bất đẳng thức tam giác: Trong một tam giác, tổng độ dài của hai cạnh bất kỳ luôn lớn hơn cạnh còn lại.
Cạnh đối diện với góc lớn hơn thì lớn hơn: Trong một tam giác, cạnh đối diện với góc lớn hơn sẽ có độ dài lớn hơn.
Các loại tam giác đặc biệt
Tam giác đều: Ba cạnh bằng nhau, ba góc bằng nhau (mỗi góc bằng 60 độ).
Tam giác cân: Có hai cạnh bằng nhau và hai góc ở đáy bằng nhau.
Tam giác vuông: Là tam giác có một góc bằng một góc vuông (90 độ).
Các đường đặc biệt trong tam giác
Đường cao: Đoạn thẳng vuông góc kẻ từ một đỉnh đến cạnh đối diện.
Đường trung tuyến: Là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện.
Đường phân giác: Đoạn thẳng chia một góc thành hai góc bằng nhau.
Đường trung trực: Là đường thẳng đi qua trung điểm của một cạnh và vuông góc với cạnh đó.
Tham khảo: Bảng đơn vị đo độ dài lớp 3
Tính chất của tam giác
Diện tích tam giác thường tính như thế nào
Công thức cơ bản
S = (a x h) / 2
Trong đó:
S: Diện tích tam giác
a: Độ dài đáy của tam giác
h: Chiều cao tương ứng với đáy a
Công thức Heron
Áp dụng khi biết độ dài ba cạnh a, b, c của tam giác.
S = √[p(p-a)(p-b)(p-c)]
Trong đó:
p = (a+b+c)/2 là nửa chu vi tam giác.
Công thức liên quan đến bán kính đường tròn nội tiếp
S = pr
Trong đó:
p: Nửa chu vi tam giác
r: Bán kính của đường tròn được nội tiếp trong tam giác.
Công thức liên quan đến bán kính đường tròn ngoại tiếp
S = abc / 4R
Trong đó:
a,b,c: Độ dài ba cạnh của tam giác.
R: Bán kính của đường tròn ngoại tiếp tam giác.
Công thức sử dụng tích có hướng (trong không gian 3 chiều)
S = 1/2 |AB x AC|
Trong đó:
AB, AC: Các vectơ biểu diễn hai cạnh của tam giác
|AB x AC|: Môđun của tích có hướng của hai vectơ AB và AC
Công thức sử dụng sin của một góc
S = 1/2 ab sinC
Trong đó:
a, b: Độ dài hai cạnh kề góc C
C: Góc giữa hai cạnh a và b
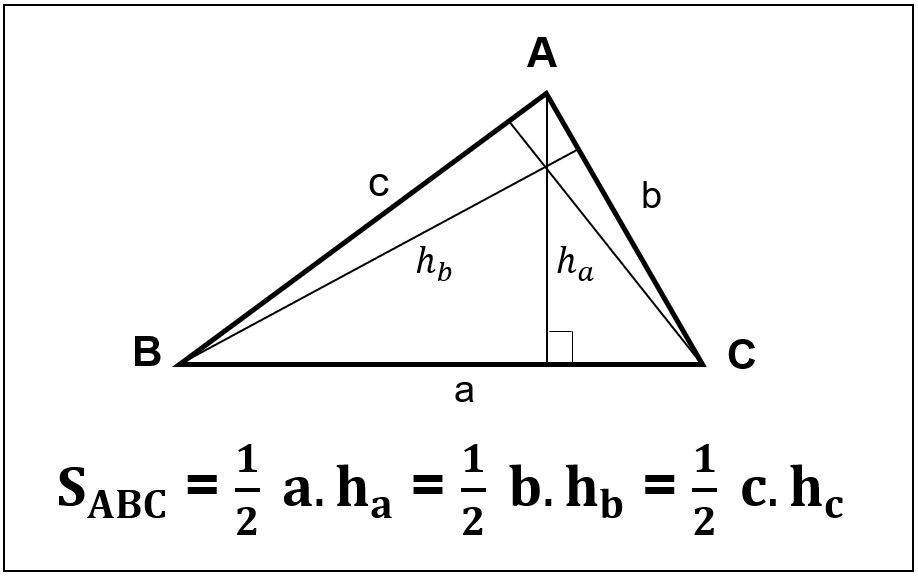
Công thức tính diện tích tam giác
Công thức tính diện tích tam giác cân, tam giác đều, tam giác vuông
Tam giác đều
Tính chất: Tam giác đều có ba cạnh bằng nhau và ba góc bằng nhau (mỗi góc bằng 60 độ).
Công thức tính diện tích tam giác đều:
S = (a²√3)/4
Trong đó:
S: Diện tích tam giác đều
a: Độ dài cạnh của tam giác đều
Tam giác cân
Tính chất: Tam giác cân có hai cạnh bằng nhau và hai góc ở đáy bằng nhau.
Công thức diện tích tam giác cân:
S = (a x h) / 2
Trong đó:
a: Độ dài đáy (cạnh không bằng hai cạnh bên)
h: Chiều cao tương ứng với đáy
Lưu ý: Để tính diện tích tam giác cân, chúng ta thường sử dụng công thức tính diện tích tam giác thường. Tuy nhiên, trong một số trường hợp, có thể áp dụng các công thức liên quan đến đường cao, đường trung tuyến, hoặc bán kính đường tròn nội tiếp, ngoại tiếp.
Tam giác vuông
Tính chất: Tam giác vuông có một góc vuông (bằng 90 độ).
Công thức:
S = (a x b) / 2
Trong đó:
a, b: Độ dài hai cạnh góc vuông
Công thức diện tích của tam giác cân
Các dạng bài tập về tính diện tích tam giác
Phương pháp tính diện tích tam giác khi biết chiều cao và độ dài đáy
Công thức: S = (a x h) / 2
Ví dụ: Cho tam giác ABC có đáy BC = 10cm, chiều cao AH = 6cm. Tính diện tích tam giác ABC.
Giải: S = (10 x 6) / 2 = 30 cm²
Cách tính diện tích tam giác khi biết ba cạnh (sử dụng công thức Heron)
Công thức: S = √[p(p-a)(p-b)(p-c)]
Trong đó:
p = (a+b+c)/2 là nửa chu vi tam giác.
Ví dụ: Cho tam giác ABC có AB = 5cm, BC = 12cm, AC = 13cm. Tính diện tích tam giác ABC.
Giải: p = (5+12+13)/2 = 15 cm. S = √[15(15-5)(15-13)(15-12)] = 30 cm²
Tính diện tích tam giác dựa vào hai cạnh và góc giữa chúng
Công thức: S = 1/2 ab sinC
Trong đó:
a, b: Độ dài hai cạnh kề góc C
C: Góc giữa hai cạnh a và b
Diện tích tam giác nội tiếp đường tròn
Công thức: S = abc / 4R
Trong đó:
a,b,c: Độ dài ba cạnh của tam giác.
Cách tính diện tích tam giác khi có được bán kính đường tròn nội tiếp
Công thức: S = pr
Trong đó:
p: Nửa chu vi tam giác
r: Bán kính của đường tròn được nội tiếp trong tam giác.
Bài toán liên quan đến tỉ số diện tích của các tam giác
Ví dụ: Cho tam giác ABC, điểm M nằm trên cạnh BC sao cho BM=2MC. So sánh diện tích của hai tam giác ABM và AMC.
Bài toán liên quan đến hình học không gian
Ví dụ: Cho hình chóp đều S.ABC có đáy ABC là tam giác đều cạnh a. Tính diện tích xung quanh và diện tích toàn phần của hình chóp.
Các dạng bài tập nâng cao
Bài toán liên quan đến hệ thức lượng trong tam giác vuông: Áp dụng định lý Pytago và các hệ thức lượng để tính toán diện tích.
Bài toán liên quan đến đường trung tuyến, đường phân giác: Sử dụng tính chất của các đường này để tính toán diện tích.
Bài toán kết hợp nhiều hình: Tính diện tích của một hình phức tạp bằng cách chia nhỏ nó thành các hình đơn giản hơn.
Bài tập mẫu tính diện tích tam giác thường, diện tích tam giác cân, tam giác đều
Bài tập 1: Tam giác vuông và đường tròn nội tiếp
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Tính bán kính đường tròn nội tiếp tam giác ABC. Từ đó tính diện tích tam giác ABC.
Bài tập 2: Tam giác đều và hình vuông
Một hình vuông có cạnh bằng a nội tiếp trong một tam giác đều. Tính diện tích phần hình tròn ngoại tiếp tam giác đều nhưng nằm ngoài hình vuông.
Bài tập 3: Tam giác và hình bình hành
Cho hình bình hành ABCD có AB = 8cm, AD = 6cm, góc BAD = 60 độ. Tính diện tích tam giác ABD.
Bài tập 4: Tam giác và đường trung tuyến
Cho tam giác ABC có trung tuyến AM. Biết AB = 10cm, AC = 6cm và AM = 8cm. Tính diện tích tam giác ABC.
Trên đây là một số thông tin về công thức tính diện tích tam giác cân, tam giác thường, tam giác đều, vuông. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.