Công thức tính đường kính hình tròn được ứng dụng rộng rãi trong toán học, kỹ thuật, xây dựng, thiên văn học, y học và đời sống hàng ngày. Hãy cùng tìm hiểu thêm qua bài viết dưới đây để nắm rõ hơn về cách áp dụng công thức này trong thực tế!
công thức tính đường kính hình tròn
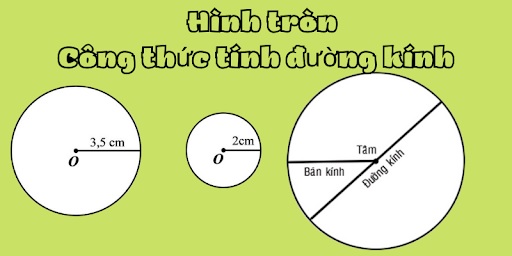
Đường kính hình tròn là gì?
Đường kính của hình tròn là đoạn thẳng nối hai điểm trên đường tròn và đi qua trung điểm của hình tròn. Đường kính là đoạn thẳng dài nhất có thể vẽ trong hình tròn.
- Đặc điểm:
- Đoạn đường kính chia hình tròn thành hai nửa bằng nhau.
- Đường kính của hình tròn là gấp đôi bán kính của nó.
Công thức tính đường kính hình tròn
Dưới đây là các công thức tính đường kính hình tròn dựa trên các yếu tố khác nhau như bán kính, chu vi và diện tích của hình tròn:
Công thức tính đường kính từ bán kính
Đây là công thức đơn giản nhất và được sử dụng khi bạn đã biết bán kính của hình tròn. Công thức tính đường kính là:
D=2r
Trong đó:
- D là đường kính của hình tròn.
- r là bán kính của hình tròn.
Bán kính là đoạn thẳng từ trung tâm của hình tròn đến một điểm trên chu vi. Đường kính chính là gấp đôi bán kính, nghĩa là đường kính luôn dài hơn bán kính một khoảng gấp đôi.
Ví dụ:
- Nếu bán kính của hình tròn là r=5 cm, thì đường kính của nó sẽ là:
D=2×5=10 cm
Đó là chiều dài lớn nhất có thể vẽ trong hình tròn.
Công thức tính đường kính từ chu vi
Chu vi của hình tròn là tổng chiều dài của toàn bộ đường biên của nó. Nếu bạn đã biết chu vi, bạn có thể tính được đường kính bằng cách sử dụng công thức sau:
D=C/π
Trong đó:
- C là chu vi của hình tròn.
- π (pi) là hằng số có giá trị xấp xỉ 3.14159.
Ví dụ:
- Nếu chu vi của hình tròn là C=31.4159 cm, ta có thể tính đường kính bằng cách:
D=31.4159 / 3.14159≈10 cm
Đây là cách sử dụng chu vi để tính toán đường kính của hình tròn.
Tham khảo: Kích thước ống hdpe
Công thức tính đường kính từ diện tích
Diện tích của hình tròn được tính bằng công thức:
A=πr²
Khi bạn biết diện tích của hình tròn, bạn có thể tính được bán kính và từ đó tính được đường kính. Đầu tiên, tính bán kính bằng cách giải phương trình diện tích, sau đó nhân với 2 để có đường kính.
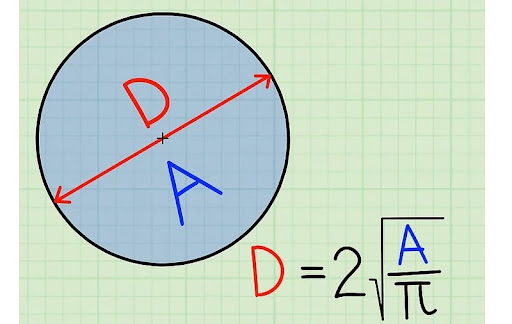
Công thức tính đường kính từ diện tích là:
D=2×√A/π
Trong đó:
- A là diện tích của hình tròn.
- π là hằng số pi (3.14159).
Ví dụ:
- Nếu diện tích của hình tròn là A=78.54 cm², ta có thể tính đường kính như sau:
D=2×√78.54/3.14159≈10 cm
Đoạn đường kính này là chiều dài lớn nhất mà bạn có thể đo trong hình tròn.
Ứng dụng của công thức tính đường kính
Công thức tính đường kính của hình tròn không chỉ là một kiến thức lý thuyết trong toán học, mà còn có nhiều ứng dụng thiết thực trong đời sống hàng ngày và các lĩnh vực kỹ thuật, sản xuất. Việc tính toán chính xác đường kính giúp giải quyết các vấn đề liên quan đến thiết kế, sản xuất và sử dụng các vật thể hình tròn. Dưới đây là một số ứng dụng quan trọng của công thức tính đường kính:
Thiết kế bánh xe và các phương tiện giao thông
- Bánh xe là một trong những ứng dụng quan trọng nhất của hình tròn. Đường kính bánh xe ảnh hưởng trực tiếp đến hiệu suất của phương tiện, như tốc độ, khả năng bám đường và độ bền của lốp. Công thức tính đường kính giúp các kỹ sư xác định kích thước bánh xe phù hợp với yêu cầu kỹ thuật của phương tiện giao thông.
- Ví dụ: Nếu bạn cần thay lốp cho xe ô tô, việc biết được đường kính bánh xe sẽ giúp bạn chọn được lốp có kích thước chính xác, đảm bảo an toàn và hiệu quả vận hành.
Kỹ thuật cơ khí và chế tạo máy
- Trong lĩnh vực chế tạo máy và cơ khí, rất nhiều bộ phận có hình dạng hình tròn như bánh răng, vòng bi, trục quay… Công thức tính đường kính giúp kỹ sư thiết kế các bộ phận này sao cho phù hợp với yêu cầu kỹ thuật và tính toán hiệu suất hoạt động.
- Ví dụ: Để chế tạo một bánh răng trong hệ thống truyền động, đường kính của bánh răng phải được tính toán chính xác để ăn khớp với các bánh răng khác, từ đó đảm bảo truyền động mượt mà và chính xác.
Thiết kế đĩa và băng đĩa (CD, DVD)
- Đĩa CD, DVD hay các thiết bị lưu trữ khác cũng có dạng hình tròn. Đường kính của chúng phải được tính toán chính xác để đảm bảo các thiết bị đọc đĩa hoạt động hiệu quả. Việc tính toán đường kính chính xác cũng giúp trong việc lưu trữ và truy xuất dữ liệu.
- Ví dụ: Trong việc sản xuất đĩa CD hoặc DVD, công thức tính đường kính giúp xác định kích thước đĩa để đảm bảo khả năng tương thích với các ổ đĩa đọc và các thiết bị lưu trữ.
Xây dựng và thiết kế hạ tầng
- Trong ngành xây dựng, đường kính được áp dụng trong thiết kế các thành phần hình tròn như cống thoát nước, ống dẫn nước, máng xối hay các cấu kiện hình tròn khác. Việc tính toán đường kính chính xác giúp đảm bảo khả năng dẫn nước hoặc chất lỏng hiệu quả, tránh tình trạng tắc nghẽn.
- Ví dụ: Khi thiết kế hệ thống cống thoát nước, các kỹ sư phải tính toán đường kính ống sao cho phù hợp với lưu lượng nước cần dẫn, từ đó đảm bảo hiệu quả và tính an toàn của hệ thống.
Ngành thực phẩm
- Trong sản xuất thực phẩm, đặc biệt là các loại bánh ngọt, pizza hay bánh tròn, việc tính toán chính xác đường kính giúp đảm bảo sản phẩm đạt chuẩn về kích thước và độ đồng đều. Đây là yếu tố quan trọng trong việc kiểm soát chất lượng sản phẩm và quy trình sản xuất.
- Ví dụ: Khi làm pizza, việc tính toán đường kính của bánh giúp đảm bảo rằng bánh có kích thước phù hợp với lò nướng và tạo ra sản phẩm đồng đều.
Trong nghiên cứu và giáo dục
- Công thức tính đường kính hình tròn là một công cụ quan trọng trong giảng dạy toán học và vật lý, giúp học sinh và sinh viên hiểu được mối quan hệ giữa các đại lượng trong hình học. Các bài toán về hình tròn, chu vi và diện tích thường sử dụng công thức tính đường kính để rèn luyện kỹ năng tính toán và suy luận.
- Ví dụ: Bài toán yêu cầu tính đường kính của một hình tròn có diện tích cho trước, sẽ giúp học sinh áp dụng công thức và phát triển kỹ năng giải quyết vấn đề.
Ứng dụng trong thể thao
- Trong một số môn thể thao như bóng đá, bóng rổ hay tennis, các thiết bị hình tròn như bóng cũng yêu cầu việc tính toán chính xác đường kính để đảm bảo phù hợp với quy chuẩn thi đấu. Đường kính của quả bóng có thể ảnh hưởng đến tính khí động học, khả năng bật nảy và cảm giác chơi.
- Ví dụ: Trong môn bóng rổ, đường kính của bóng cần phải phù hợp với kích thước của rổ để đảm bảo tính công bằng trong thi đấu.
Trong công nghệ và sản xuất vật liệu
- Các vật liệu phẳng, mỏng như tấm kim loại, tấm kính, hoặc tấm nhựa khi được cắt thành hình tròn đều cần phải xác định chính xác đường kính để đảm bảo kích thước đúng yêu cầu của sản phẩm. Công thức tính đường kính giúp trong việc tính toán số lượng vật liệu cần thiết và giảm thiểu lãng phí.
- Ví dụ: Trong sản xuất đồng hồ, các bộ phận như mặt đồng hồ hay kính đồng hồ đều có dạng hình tròn, và đường kính cần phải được tính toán tỉ mỉ để vừa vặn với vỏ đồng hồ.
Tổng kết
Trong bài viết này, TRƯỜNG THỊNH đã cung cấp những thông tin chi tiết về công thức tính đường kính hình tròn, từ định nghĩa cơ bản đến các công thức tính toán, cùng với những ứng dụng thực tế rộng rãi trong các lĩnh vực như toán học, kỹ thuật, xây dựng, thiên văn học, y học và cuộc sống hàng ngày. Công thức này không chỉ giúp chúng ta xác định kích thước của hình tròn mà còn đóng vai trò quan trọng trong việc thiết kế, đo lường và tối ưu hóa nhiều công trình và sản phẩm.
Hy vọng bài viết đã giúp bạn nắm bắt được kiến thức về đường kính hình tròn, đồng thời biết cách áp dụng công thức này một cách hiệu quả trong các tình huống thực tế. Chúc bạn học tốt và vận dụng thành công trong các lĩnh vực liên quan!






